Решение матричной игры в смешанных стратегиях

Если платежная матрица не имеет седловой точки, т.е. a<b и a ≤ n ≤ b, то поиск решения игры приводит к применению сложной стратегии, состоящей в случайном применении двух и более стратегий с определенными частотами.

Определение Сложная стратегия, состоящая в случайном применении всех стратегий с определенными частотами, называется смешанной.

В игре, матрица которой имеет размерность , стратегии первого игрока задаются наборами вероятностей , с которыми игрок применяет свои чистые стратегии.

Эти наборы можно рассмотреть как m-мерные векторы, для координат которых выполняются условия

Аналогично для второго игрока наборы вероятностей определяют n-мерные векторы 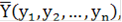для координат которых выполняются условия

Выигрыш первого игрока при использовании смешанной стратегии определяют как математическое ожидание выигрыша, т.е. он равен

Теорема Неймана (основная теорема теории игр). Каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий.

Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры:

a ≤ n ≤ b.

Применение первым игроком оптимальной стратегии должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры. Поэтому выполняется соотношение

Аналогично для второго игрока оптимальная стратегия должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры, т.е. справедливо соотношение

Если платежная матрица не содержит седловой точки, то задача определения смешанной стратегии тем сложнее, чем больше размерность матрицы.

оэтому матрицы большой размерности целесообразно упростить, уменьшив их размерность путем вычеркивания дублирующих и не доминирующих стратегий.

Определение Если все элементы i-й строки платежной матрицы больше соответствующих элементов k-й строки, то i-я стратегия игрока A называется доминирующей над k-й стратегией.

Если все элементы j-го столбца платежной матрицы меньше соответствующих элементов k-го столбца, то j-я стратегия игрока В называется доминирующей над k-й стратегией.

Пример:

Рассмотрим игру, представленную платежной матрицей

Все элементы стратегии заведомо невыгодны для первого игрока и ее можно исключить.

Все элементы меньше, исключаем

Для второго игрока: сравнивая и , исключаем ; сравнивая и , исключаем сравнивая и , исключаем В результате преобразований получим матрицу