Эконометрические модели

Традиционные модели временных рядов, такие как модель ARMA, не могут адекватно учесть все характеристики, которыми обладают финансовые временные ряды, и требуют расширения. Одна из характерных черт финансовых рынков - это то, что присущая рынку неопределенность изменяется во времени. Как следствие, наблюдается «кластеризация волатильности». Под этим имеется в виду то, что могут чередоваться периоды, когда финансовый показатель ведет себя непостоянно, и относительно спокойные периоды. Эффект кластеризации волатильности отмечен для таких рядов как изменение цен акций, валютных курсов, доходности спекулятивных активов. Применением ARCH моделей установлено, что динамика волатильности многих финансовых переменных

подчиняется устойчивым закономерностям. Ключевой момент, предлагаемый ARCH моделью, состоит в различении условных и безусловных моментов второго порядка. В то время как безусловная матрица ковариаций для представляющих интерес переменных может быть неизменной во времени, условные дисперсии и ковариации часто зависят нетривиальным образом от состояний мира в прошлом. Понимание точного характера этой временной зависимости крайне важно для многих проблем в макроэкономике и финансах, в том числе и для проблем фондового рынка. Кроме того, с точки зрения получения эконометрических выводов потеря асимптотической эффективности из-за неучета гетероскедастичности может быть сколь угодно большой, и при составлении экономических прогнозов, как правило, можно использовать намного более точную оценку неопределенности ошибки прогноза, если получать ее как условную по текущему информационному множеству.

ARCH-модель моделирует волатильность в виде суммы константной базовой волатильности и линейной функции абсолютных значений нескольких последних изменений цен. При этом уровень волатильности (стандартное отклонение доходности финансового инструмента) рассчитывается по следующей рекурсивной формуле (ARCH(q)):

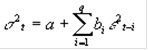, где- константа, базовая волатильность; i - предыдущие изменения цен; q - порядок модели - количество последних изменений цен, влияющих на текущую волатильность; bi - весовые коэффициенты, определяющие степень влияния предыдущих изменений цен на текущее значение волатильности.

Расширением ARCH-модели является GARCH-модель волатильности, где на текущую волатильность влияют как предыдущие изменения цен, так и предыдущие оценки волатильности (т.н. "старые новости"). Согласно данной модели (GARCH(p, q)) расчет волатильности производится по следующей формуле:

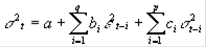
где p - количество предшествующих оценок волатильности, влияющих на текущую; ci - весовые коэффициенты, определяющие степень влияния предыдущих оценок волатильности на текущее значение.

Высокие по абсолютному значению реализации процесса в непосредственном прошлом влекут увеличение условной дисперсии в данный момент, и, следовательно, условной вероятности появления вновь высокой по модулю реализации ε. Напротив, относительно небольшие значения εt-1, .,εt-q приводят к снижению этой вероятности. Таким образом, можно ожидать, что вслед за большими (по абсолютному значению) наблюдениями вновь последуют большие наблюдения, за малыми - малые. Выбросы имеют тенденцию следовать один за другим, формируя периоды экстремально высокой волатильности.модель позволяет обойти проблему длинных лагов и большого числа параметров, ее применение успешно идентифицирует толстые хвосты и кластеризацию волотильности. Простая структура GARCH-модели существенно ограничивает динамику временного ряда. Как правило указывают на три недостатка данного типа. Первый связан с тем, что GARCH-модель игнорирует корреляцию между εt и σ2t+1. Второй недостаток происходит от того, что применительно к процессам типа GARCH различные определения стационарности не согласованы. Наконец, ограничения области допустимых значений параметров α и β создают трудности при оценивании GARCH модели. Модель GARCH можно модифицировать, чтобы учесть и некоторые другие особенности. В экспоненциальной GARCH-модели (EGARCH) , предложенной Нельсоном σ2t зависит как от абсолютного размера, так и от знака лагов остатков. А именно: