Склады.

;

.

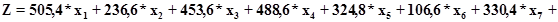
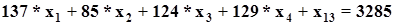Коэффициент при искусственной переменных в целевой функции равен -М так как задача на максимум.

Вводим недостающие единичные вектора:

,

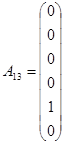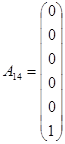
Исходя из всего, проделанного ранее, формируем исходный опорный план:

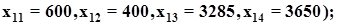
при заданном исходном опорном плане целевая функция примет следующий вид:

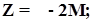
. Нахождение оптимального плана работы флота и оптимальных схем движения судов

Используя программу ПЭР получаем, что искусственные переменные равны 0, все оценки векторов условий в m+2 строке положительны, следовательно, найден оптимальный план при котором целевая функция достигает своего максимума:

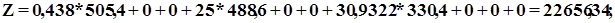Х1=0,438; Х2= 0; Х3=0; Х4=25; Х5=0; Х6=0; Х7=30,9322; Х8=0;

Таблица 4.1