|
. построить графики изменения фазовых координат системы во времени при переходе системы из начального состояния в конечное за минимальное время;
. построить графики изменения оптимального управления во времени, обеспечивающего минимальное время перехода из исходного состояния в конечное;
. построить графики изменения фазовых координат системы во времени при переходе системы из исходного состояния системы в конечное;
. построить графики изменения неоптимального управляющего воздействия.
.3 Решение задачи принципом максимума
 (6.7) (6.7)
В данной задаче:
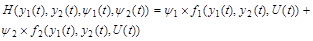 (6.8) (6.8)
С учетом конкретного математического описания системы (6.3) и (6.4) функция Гамильтона принимает вид:
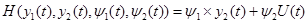 (6.9) (6.9)
Система дифференциальных уравнений, сопряженных системе (6.3) и (6.4) имеет вид:
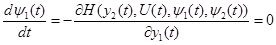 (6.10) (6.10)
 (6.11) (6.11)
Согласно принципу максимума при оптимальном управлении функция Гамильтона (9) принимает максимальное значение. Следовательно, для поиска оптимального управления Uопт(t), нужно максимизировать функцию Гамильтона:
 (6.12) (6.12)
Так как функция Гамильтона (6.9) линейно зависит от управления U(t), то оптимальное управление будет принимать значения: Uопт(t)=-1, если множитель при U(t) в (6.9) имеет знак «-»; и Uопт(t)=1, если множитель при U(t) в (6.9) имеет знак «+», т.е.: Uопт(t)=signΨ2(t), где signΨ2(t) - знаковая функция.
В соответствии с алгоритмом решения задачи принципом максимума найденное выражение оптимального управления подставляют в систему сопряженных уравнений (6.3), (6.4), (6.10), (6.11).
Решение этой системы при заданных граничных условиях (6.5а), (6.5б), (6.5в) и (6.5г) можно получить в фазовом пространстве
 (6.14) (6.14)
или во временной области
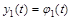 (6.15) (6.15)
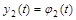 (6.16) (6.16)
При решении системы уравнений (6.3), (6.4), (6.10), (6.11) в фазовом пространстве оптимальное управление является функцией фазовых координат. При решении системы уравнений (6.3), (6.4), (6.10), (6.11) во временной области оптимальное управление является функцией времени. Покажем это: рассмотрим систему уравнений (6.10) и (6.11).
Из (6.10) следует:
 (6.17) (6.17)
Подставим (6.17) в (6.11):
 (6.18) (6.18)
и проинтегрируем (6.18)
 (6.19) (6.19)
Заметим, что функция (6.19) линейна. Следовательно, Ψ2(t) только один раз может сменить знак (рис. 1).


Рис. 1. Графики функций Ψ2(t) и Uопт(t)
В соответствии с (6.13) оптимальное управление тоже только один раз меняет знак и может переключаться со значения (-1) на (+1) или со значения (+1) на (-1).
.4 Построение фазовых траекторий.
Построим фазовые траектории движения системы для случая Uопт(t)=+1. При этом система уравнений (3) и (4) описывающая рассматриваемую систему, примет вид:
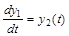 (6.20) (6.20)
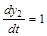 (6.21) (6.21)
Поделим (6.20) на (6.21):
 (6.22) (6.22)
и проинтегрируем (6.22):
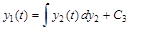 (6.23) (6.23)
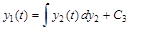
 (6.24) (6.24)
Уравнение (6.24) описывает движение системы в фазовом пространстве при U(t)=1. Графики функции (6.24) для различных y0 приведены на рис.2. Они представляют собой параболы с ветвями симметричными относительно оси y1(t), и вершинами слева.
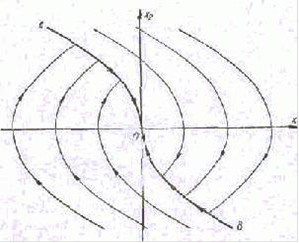
Рис. 2. Графики движения системы в фазовом пространстве в зависимости от начальных условий и функции управления.
|