|
Значение функции в новой точке F(X,Y) = -4910,74911252246
Проверка удачности шага.
Так как F(Xновое, Yновое) = -4910,74911252246>=F(X, Y) = -4910,74911253306
то делим шаг пополам.
Новый шаг h = 0,00078125
Так как текущее значение h < sig (0,001), то приравниваем h к h0.
Шаг 11451
Делаем шаг из точки X = -357,148864228791 Y = 69,5297901322648
Функция F(X, Y) в данной точке = -4910,74911253306
Текущий шаг h = 0,1
Значение функции в текущей точке F(X, Y) = -4910,74911253306
Значение частной производной по x  = 0,00054540578275919 = 0,00054540578275919
Значение частной производной по y  = 0,066409120336175 = 0,066409120336175
Проверка на выход.
Корень суммы квадратов частных производных A = 0,0664113599566553
Так как A (0,0664113599566553) <= E (0,1) то поиск окончен.

График функции
Итоговая таблица |
№ метода |
Название метода |
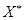    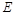 Кол-во шагов Кол-во шагов
|
Кол-во вычислений целевой функции |
|
|
|
| |
1 |
Аналитический метод |
-357,01 |
69,50 |
-4910,74 |
- |
- |
- | |
2 |
Метод Гаусса - Зейделя |
-359,91 |
70,08 |
-4910,40 |
0,1 |
2972 |
3328 | |
3 |
Метод Градиента |
-358,28 |
69,75 |
-4910,68 |
0,1 |
2455 |
7366 | |
4 |
Метод Наискорейшего спуска |
-357,14 |
69,52 |
-4910,74 |
0,1 |
11451 |
45817 |
Вывод: Сравнив результаты, полученные при вычислении экстремума функции численными методами с результатами аналитического метода получили, что численные методы дают приблизительное значение экстремума функции, близкое к точному. Из численных методов самым эффективным оказался метод Градиента.
ЛАБОРАТОРНАЯ РАБОТА №5
Решение задачи оптимального вложения инвестиций, как задачи распределения, методом динамического программирования
.1 Постановка задачи
Задан объем инвестиций А = 5. Требуется оптимально распределить этот объем на три мероприятия. Эффективность каждого мероприятия от вложенных инвестиций оценивается величиной прибыли qi(Ui).
 (5.1) (5.1)
А - общий объем инвестиций;
Ui = 0, 1, 2, 3, 4, 5 - объем инвестиций в каждое мероприятие;
qi(Ui) - эффективность вложенных средств, которая выражается в виде составляющей эффекта вложенных средств (результат вложения средств в i-тое мероприятие - прибыль).
Нам даны следующие значения:
q1(U1) = 1,2*0,2*U1 =0,24 U1.
|
U2 |
0 |
1 |
2 |
3 |
4 |
5 | |
q2 |
0 |
0,09 |
0,405 |
0,45 |
0,54 |
0,63 | |
U3 |
0 |
1 |
2 |
3 |
4 |
5 | |
q3 |
0 |
0,55 |
0,715 |
0,825 |
0,88 |
0,935 |
|