|
|
3 шаг |
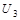   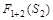 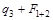 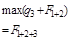
|
|
|
|
|
| |
S3=A |
0 |
0 |
5 |
1,2 |
1,2 |
1,51 | |
|
1 |
0,55 |
4 |
0,96 |
1,51 |
| |
|
2 |
0,715 |
3 |
0,72 |
1,435 |
| |
|
3 |
0,825 |
2 |
0,48 |
1,305 |
| |
|
4 |
0,88 |
1 |
0,24 |
1,12 |
| |
|
5 |
0,935 |
0 |
0 |
0,935 |
|
В результате проделанных расчетов получено оптимальное распределение инвестиций объемом в 5 единиц на три мероприятия следующим образом:
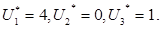
Таким образом, следует в первое мероприятие вложить 4 единицы инвестиций и в третье - 1 единицу.
ЛАБОРАТОРНАЯ РАБОТА №6
Решение классической задачи синтеза оптимального управления с использованием принципа максимума
.1 Постановка задачи
Требуется минимизировать время перехода системы из начального состояния y1(0)=ya0 в конечное y(tk)=yk.
Система описывается дифференциальным уравнением:
 (6.1) (6.1)
где y(t) - фазовая координата, а U(t) - управляющее воздействие
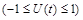
6.2 Постановка задачи в математической форме.
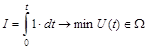 (6.2) (6.2)
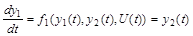 (6.3) (6.3)
 (6.4) (6.4)
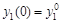 (6.5а) (6.5а)
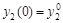 (6.5б) (6.5б)
 (6.5в) (6.5в)
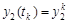 (6.5г) (6.5г)
 (6.6) (6.6)
Область допустимых управлений 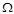 удовлетворяет условию (6.6). удовлетворяет условию (6.6).
Требуется для заданных начальных [(6.5а) и (6.5б)] и конечных [(6.5в) и (6.5г)] граничных условий состояния системы:
1. построить траекторию движения системы в фазовом пространстве, обеспечивающую минимальное время перехода из начального в конечное;
2. траекторию неоптимального движения системы в фазовом пространстве;
|