|
5.2 Метод решения
Данную задачу следует решать методом динамического программирования.
В основе динамического программирования лежит принцип оптимальности: “Оптимальная стратегия обладает тем свойством, что каковы бы ни были первоначальное состояние и управление, при которых система пришла в это состояние, последующее решение (управления) должны быть оптимальными по отношению к этому состоянию.
Сущность динамического программирования состоит в том, что задача большой размерности разбивается на ряд подзадач меньшей размерности (проводится декомпозиция). Это достигается разбивкой всего процесса на несколько стадий. Процесс решения задачи выполняется пошагово. На первом шаге вычисляют значение составляющей критерия оптимальности от одной стадии. На втором и последующих шагах оптимизируется суммарное приращение критерия оптимальности от вновь вводимой стадии процесса вместе с полученным результатом оптимизации на предыдущем шаге. Математически это представляется следующим образом.
Пусть критерий оптимальности имеет вид
 (5.2) (5.2)
где Si,Ui - соответственно состояние и управление i-ой стадии процесса. (i=1,2,…,N).
Последующие состояния определяются выражениями:
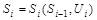 (5.3) (5.3)
Первый шаг оптимизации опишем выражением
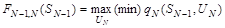
Второй и последующий шаги описываются рекуррентным уравнением
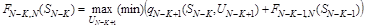 (5.4) (5.4)
Выражения (5.3) и (5.4) называются функциональными уравнениями динамического программирования.
Пример выполнения задания:
шаг.
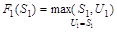
шаг.
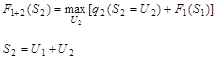
шаг.
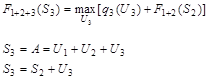
5.3 Результаты расчетов
|
1 шаг |
U1 |
 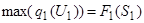
|
|
| |
S1 |
 0 0
|
0 |
|
| |
|
 0,24 0,24
|
0,24 |
|
| |
|
 0,48 0,48
|
0,48 |
|
| |
|
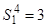 0,72 0,72
|
0,72 |
|
| |
|
 0,96 0,96
|
0,96 |
|
| |
|
 1,2 1,2
|
1,2 |
|
| |
|
|
|
|
| |
2 шаг |
 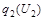 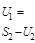 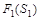 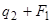 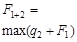
|
|
|
|
|
|
| |
S2=X |
 0 0
|
0 |
0 |
0 |
0 |
0 |
|
| |
|
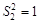 0 0
|
0 |
1 |
0,24 |
0,24 |
0,24 |
|
| |
|
|
1 |
0,1 |
0 |
0 |
0,1 |
|
| |
|
 0 0
|
0 |
2 |
0,48 |
0,48 |
0,48 |
|
| |
|
|
1 |
0,09 |
1 |
0,24 |
0,33 |
|
| |
|
|
2 |
0,405 |
0 |
0 |
0,405 |
|
| |
|
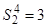 0 0
|
0 |
3 |
0,72 |
0,72 |
0,72 |
|
| |
|
|
1 |
0,09 |
2 |
0,48 |
0,57 |
|
| |
|
|
2 |
0,405 |
1 |
0,24 |
0,645 |
|
| |
|
|
3 |
0,45 |
0 |
0 |
0,45 |
|
| |
|
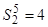 0 0
|
0 |
4 |
0,96 |
0,96 |
0,96 |
|
| |
|
|
1 |
0,09 |
3 |
0,72 |
0,81 |
|
| |
|
|
2 |
0,405 |
2 |
0,48 |
0,885 |
|
| |
|
|
3 |
0,45 |
1 |
0,24 |
0,69 |
|
| |
|
|
4 |
0,54 |
0 |
0 |
0,54 |
|
| |
|
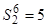 0 0
|
0 |
5 |
1,2 |
1,2 |
1,2 |
|
| |
|
|
1 |
0,09 |
4 |
0,96 |
1,05 |
| |
|
|
2 |
0,405 |
3 |
0,72 |
1,125 |
| |
|
|
3 |
0,45 |
2 |
0,48 |
0,93 |
| |
|
|
4 |
0,54 |
1 |
0,24 |
0,78 |
| |
|
|
5 |
0,63 |
0 |
0 |
0,63 |
| | | | | | | | | | | | | | | | | | | | |
|