|
Построим фазовые траектории движения системы для случая Uопт(t)=-1. При этом система уравнений (3) и (4), описывающая рассматриваемую систему, примет вид:
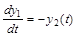 (6.25) (6.25)
 (6.26) (6.26)
Решение системы уравнений (6.25) и (6.26) найдем аналогично предыдущему случаю:
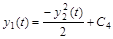 (6.27) (6.27)
Графики функций для различных y0 приведены на рис. 2. Они представляют собой параболы с ветвями, симметричными относительно оси y1(t), и вершинами справа.
Заметим, что фазовая координата y2(t) является скоростью изменения фазовой координаты y1(t). Поэтому в положительной полуплоскости относительно оси y1(t) (т.е. для y2(t)>0) координата y1(t) может только возрастать, а в отрицательной полуплоскости относительно оси y1(t) (т.е. для y2(t)<0) координата y1(t) может только убывать.
Геометрически задача оптимального управления сводится к тому, что из заданной исходной точки фазового пространства с координатами (y10, y20) нужно перейти в заданную конечную точку с координатами (y1k, y2k) и при этом осуществить лишь один переход с одной траектории, проходящей через точку с координатами (y10, y20) на траекторию с координатами (y1k, y2k). Если переход из начальной точки в конечную выполнен при числе переходов с одной траектории на другую больше одного, то в данной задаче управление выбрано не оптимальным.
Пусть конечным состоянием является начало координат (y10=0, y20=0). Полуветви парабол, по которым можно попасть в точку (y10=0, y20=0), образует линию переключения, которую обозначим MON. Уравнение линии переключения в этом случае имеет вид:
y1=-y22/2*sign(y2(t))(28)
Задача на максимальное быстродействие будет решена, если из начальной точки выбирается управление, при котором обеспечивается выход на линию переключения. При встрече с этой линией осуществляется переключение знака управления на противоположный, что обеспечивает переход на линию переключения и спуск по ней в конечную точку.
Причем, если начальная точка расположена правее линии переключения, то движение из нее нужно осуществлять при U=1. Если начальная точка расположена правее линии переключения, то движение из нее нужно осуществить при U=-1.
Таким образом, оптимальное управление формируется условиями:
· Если y1(t)<-y22/2*sign(y2(t)), то Uопт(t)=1(29)
· Если y1(t)>-y22/2*sign(y2(t)), то Uопт(t)=-1(30)
В том случае, если начальная точка расположена на линии переключения, т.е. y1(t)=-y22/2*sign(y2(t)), то Uопт(t)=1 (31); если y2(t)<0 или Uопт(t)=-1, если y2(t)>0 (32).
В этом случае переключения знака управления не требуется. Математически это означает, что за время перехода из начальной точки в конечную функция Ψ2(t) не изменяла знак.
Результатом моделирования оптимального перехода системы из заданного начального в заданное конечное состояние являются графики движения системы в фазовом пространстве и во временной области. Начальное и конечное состояния системы задаются преподавателем.
|